In the first part of my somehow lengthy comparison between Fortran, ILNumerics, Matlab and numpy, I gave some categorization insight into terms related to ‘performance’ and ‘language’. This part explains the setup and hopefully the results will fit in here as well (otherwise we’ll need a third part ![]() )
)
Prerequisites
This comparison is going to be easy and fair! This means, we will not attempt to compare an apple with the same apple, wrapped in a paper bag (like often done with the MKL) nor are we going to use specific features of an individual language/ framework – just to outperform another framework (like using datastructures which are better handled in a OOP language, lets say complicated graph structures or so).
We rather seek for an algorithm of:
- Sufficient size and complexity. A simple binary function like BLAS: DAXPY is not sufficient here, since it would neglect the impact of the memory management – a very important factor in .NET.
- Limited size and complexity in order to be able to implement the algorithm on all frameworks compared (in a reasonable time).
We did chose the kmeans algorithm. It only uses common array syntax, no calls to linear algebra routines (which are usually implemented in Intel’s MKL among all frameworks) and – used on reasonable data sizes – comes with sufficient complexity, computational and memory demands. That way we can measure the true performance of the framework, its array implementation and the feasibility of the mathematical syntax.
Two versions of kmeans were implemented for every framework: A ‘natural’ version which is able to be translated into all languages with minimal differences according execution cost. A second version allows for obvious optimizations to get applied to the code according the language recommendations where applicable. All ‘more clever’ optimizations are left to the corresponding compiler/interpreter.
The test setup: Acer TravelMate 8472TG, Intel Core™ i5-450M processor 2.4GHz, 3MB L3 cache, 4GB DDR3 RAM, Windows 7/64Bit. All tests were targeting the x86 platform.
ILNumerics Code
The printout of the ILNumerics variant for the kmeans algorithm is shown. The code demonstrates only obligatory features for memory management: Function and loop scoping and specific typed function parameters. For clarity, the function parameter checks and loop parameter initialization parts have been abbreviated.
public static ILRetArray<double> kMeansClust (ILInArray<double> X,
ILInArray<double> k,
int maxIterations,
bool centerInitRandom,
ILOutArray<double> outCenters) {
using (ILScope.Enter(X, k)) {
// … (abbreviated: parameter checking, center initializiation)
while (maxIterations --> 0) {
for (int i = 0; i < n; i++) {
using (ILScope.Enter()) {
ILArray<double> minDistIdx = empty();
min(sum(abs(centers - X[full,i])), minDistIdx,1).Dispose();// **
classes[i] = minDistIdx[0];
}
}
for (int i = 0; i < iK; i++) {
using (EnterScope()) {
ILArray<double> inClass = X[full,find(classes == i)];
if (inClass.IsEmpty) {
centers[full,i] = double.NaN;
} else {
centers[full,i] = mean(inClass,1);
}
}
}
if (allall(oldCenters == centers)) break;
oldCenters.a = centers.C;
}
if (!object.Equals(outCenters, null))
outCenters.a = centers;
return classes;
}
}
The algorithm iteratively assigns data points to cluster centres and recalculates the centres according to its members afterwards. The first step needs n * m * k * 3 ops, hence its effort is O(nmk). The second step only costs O(kn + mn), hence the first loop clearly dominates the algorithm. A version better taking into account available ILNumerics features, would replace the line marked with ** by the following line:
... min(distL1(centers, X[full, i]), minDistIdx, 1).Dispose(); ...
The distL1 function basically removes the need for multiple iterations over the same distance array by condensing the element subtraction, the calculation of the absolute values and its summation into one step for every centre point.
Matlab® Code
For the Matlab implementation the following code was used. Note, the existing kmeans algorithm in the stats toolbox has not been utilized, because it significantly deviates from our simple algorithm variant by more configuration options and inner functioning.
function [centers, classes] = kmeansclust (X, k, maxIterations,
centerInitRandom)
% .. (parameter checking and initialization abbreviated)
while (maxIterations > 0)
maxIterations = maxIterations - 1;
for i = 1:n
dist = centers - repmat(X(:,i),1,k); % ***
[~, minDistIdx] = min(sum(abs(dist)),[], 2);
classes(i) = minDistIdx(1);
end
for i = 1:k
inClass = X(:,classes == i);
if (isempty(inClass))
centers(:,i) = nan;
else
centers(:,i) = mean(inClass,2);
inClassDiff = inClass - repmat(centers(:,i),1,size(inClass,2));
end
end
if (all(all(oldCenters == centers)))
break;
end
oldCenters = centers;
end
Again, a version better matching the performance recommendations for the language would prevent the repmat operation and reuse the single column of X for all centres in order to calculate the difference between the centres and the current data point.
... dist = bsxfun(@minus,centers,X(:,i)); ...
FORTRAN Code
In order to match our algorithm most closely, the first FORTRAN implementation simulates the optimized bsxfun variant of Matlab and the common vector expansion in ILNumerics accordingly. The array of distances between the cluster centres and the current data point is pre-calculated for each iteration of i:
subroutine SKMEANS(X,M,N,IT,K,classes)
!USE KERNEL32
!DEC$ ATTRIBUTES DLLEXPORT::SKMEANS
! DUMMIES
INTEGER :: M,N,K,IT
DOUBLE PRECISION, INTENT(IN) :: X(M,N)
DOUBLE PRECISION, INTENT(OUT) :: classes(N)
! LOCALS
DOUBLE PRECISION,ALLOCATABLE :: centers(:,:) &
,oldCenters(:,:) &
,distances(:) &
,tmpCenter(:) &
,distArr(:,:)
DOUBLE PRECISION nan
INTEGER S, tmpArr(1)
nan = 0
nan = nan / nan
ALLOCATE(centers(M,K),oldCenters(M,K),distances(K),tmpCenter(M),distArr(M,K))
centers = X(:,1:K) ! init centers: first K data points
do
do i = 1, N ! for every sample...
do j = 1, K ! ... find its nearest cluster
distArr(:,j) = X(:,i) - centers(:,j) ! **
end do
distances(1:K) = sum(abs(distArr(1:M,1:K)),1)
tmpArr = minloc ( distances(1:K) )
classes(i) = tmpArr(1);
end do
do j = 1,K ! for every cluster
tmpCenter = 0;
S = 0;
do i = 1,N ! compute mean of all samples assigned to it
if (classes(i) == j) then
tmpCenter = tmpCenter + X(1:M,i);
S = S + 1;
end if
end do
if (S > 0) then
centers(1:M,j) = tmpCenter / S;
else
centers(1:M,j) = nan;
end if
end do
if (IT .LE. 0) then ! exit condition
exit;
end if
IT = IT - 1;
if (sum(sum(centers - oldCenters,2),1) == 0) then
exit;
end if
oldCenters = centers;
end do
DEALLOCATE(centers, oldCenters,distances,tmpCenter);
end subroutine SKMEANS
Another version of the first step was implemented which utilizes the memory accesses more efficiently. Its formulation relatively closely matches the ‘optimized’ version of ILNumerics:
...
do i = 1, N ! for every sample...
do j = 1, K ! ... find its nearest cluster
distances(j) = sum( &
abs( &
X(1:M,i) - centers(1:M,j)))
end do
tmpArr = minloc ( distances(1:K) )
classes(i) = tmpArr(1);
end do
...
numpy Code
The general variant of the kmeans algorithm in numpy is as follows:
from numpy import *
def kmeans(X,k):
n = size(X,1)
maxit = 20
centers = X[:,0:k].copy()
classes = zeros((1.,n))
oldCenters = centers.copy()
for it in range(maxit):
for i in range(n):
dist = sum(abs(centers - X[:,i,newaxis]), axis=0)
classes[0,i] = dist.argmin()
for i in range(k):
inClass = X[:,nonzero(classes == i)[1]]
if inClass.size == 0:
centers[:,i] = np.nan
else:
centers[:,i] = inClass.mean(axis=1)
if all(oldCenters == centers):
break
else:
oldCenters = centers.copy()
Since this framework showed the slowest execution speed of all implemented frameworks in the comparison (and due to my limited knowledge of numpys optimization recommendations) no improved version was sought.
Parameters
The 7 algorithms described above were all tested against the same data set of corresponding size. Test data were evenly distributed random mumbers, generated on the fly and reused for all implementations. The problem sizes m and n and the number of clusters k are varied according the following table:
min value max value fixed parameters m 50 2000 n = 2000, k = 350 n 400 3000 m = 500, k = 350 k 10 1000 m = 500, n = 2000
By varying one value, the other variables were fixed respectively.
The results produced by all implementations were checked for identity. Each test was repeated 10 times (5 times for larger datasets) and the average of execution times were taken as test result. Minimum and maximum execution times were tracked as well.
Results
Ok, I think we make it to the results in this part! ![]() The plots first! The runtime measures are shown in the next three figures as error bar plots:
The plots first! The runtime measures are shown in the next three figures as error bar plots:
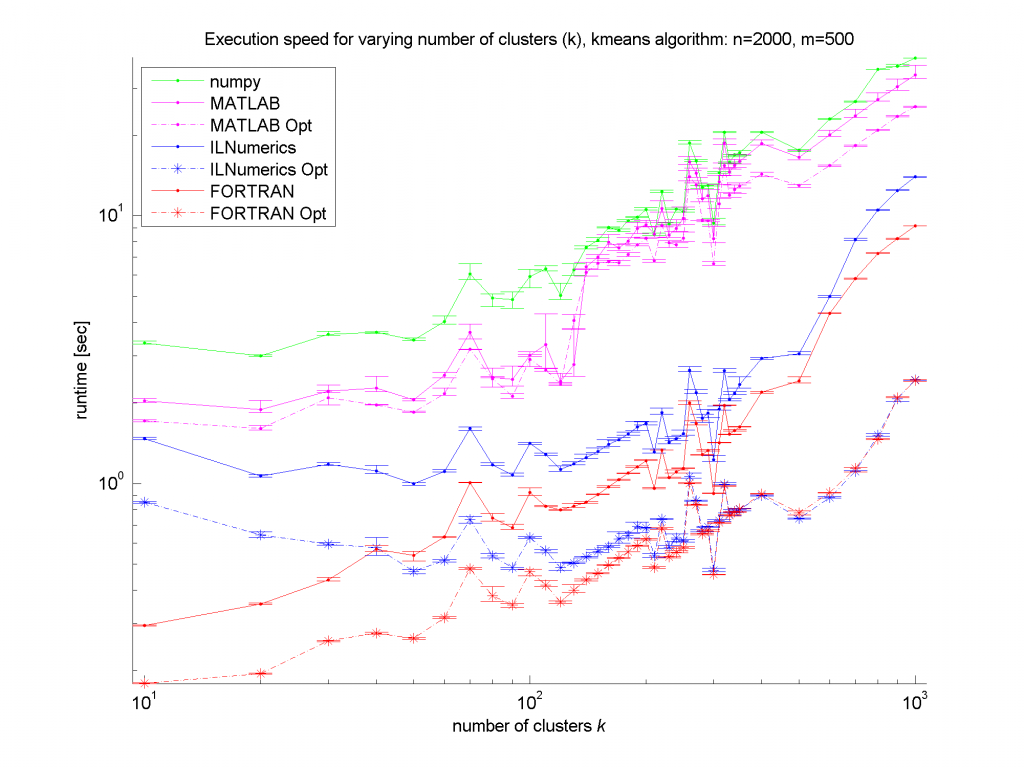
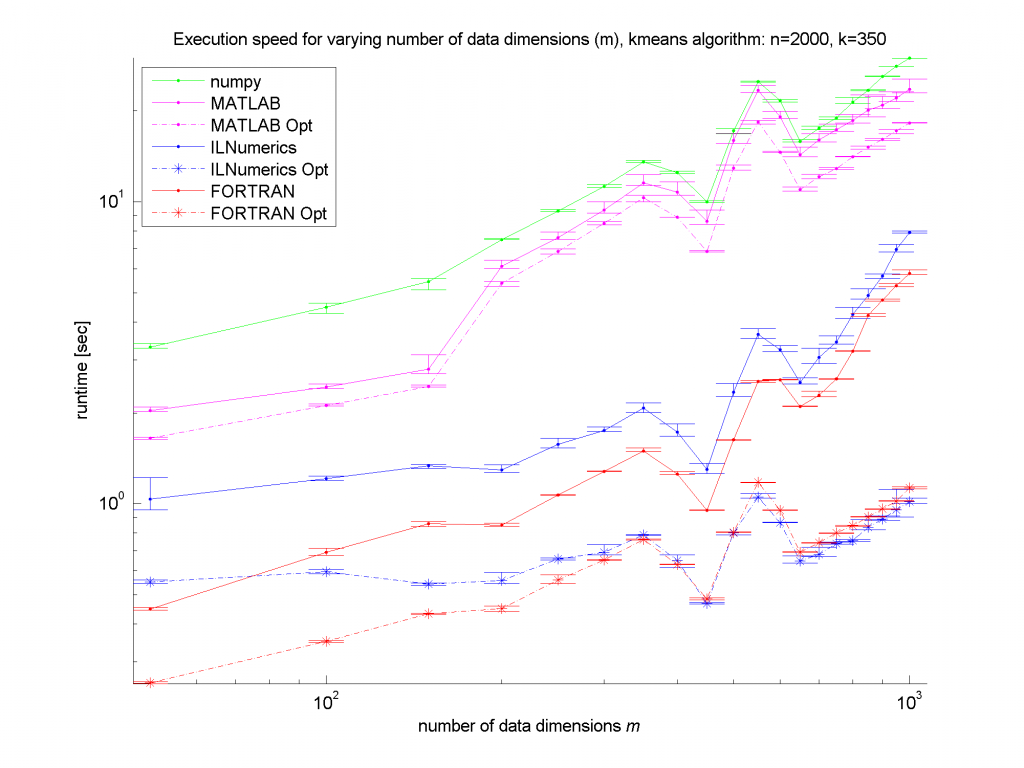
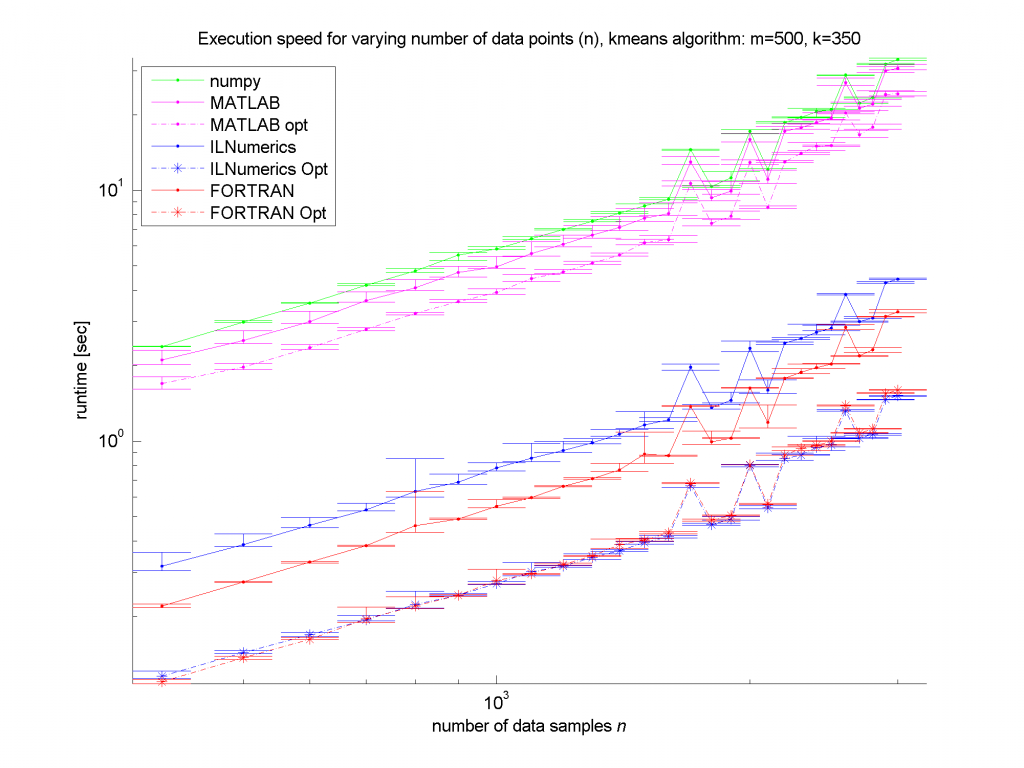
Clearly, the numpy framework showed the worst performance – at least we did not implement any optimization for this platform. MATLAB, as expected, shows similar (long) execution times. In the case of the unoptimized algorithms, the ILNumerics implementation is able to almost catch up with the execution speed of FORTRAN. Here, the .NET implementation needs less than twice the time of the first, naïve FORTRAN algorithm. The influence of the size of n is negligible, since the most ‘work’ of the algorithm is done by calculating the distances of one data point to all cluster centres. Therefore, only the dimensionality of the data and the number of clusters are important here.
Conclusion
For the optimized versions of kmeans (the stippled lines in the figures) – especially for middle sized and larger data sets (k > 200 clusters or m > 400 dimensions) – the ILNumerics implementation runs at the same speed as the FORTRAN one. This is due to ILNumerics implementing similar optimizations into its builtin functions as the FORTRAN compiler does. Also, the efforts of circumventing around the GC by the ILNumerics memory management and preventing from bound checks in inner loops pay off here. However, there is still potential for future speed-up, since SSE extensions are (yet) not utilized.
For smaller data sets, the overhead of repeated creation of ILNumerics arrays becomes more important, which will be another target for future enhancements. Clearly visible from the plots is the high importance of the choice of algorithm. By reformulating the inner working loop, a significant improvement has been achieved for all frameworks.

