Next to other great improvements in version 4.10 of ILNumerics Ultimate VS, it is especially one new feature which requires some attention: general broadcasting for n-dimensional ILArrays.
Broadcasting as a concept today is found in many popular mathematical prototyping systems. The most direct correspondence probably exists in the numpy package. Matlab and Octave offer similar functionality by means of the bsxfun function.
The term ‘broadcasting’ refers to a binary operator which is able to apply an elementwise operation to the elements of two n-dimensional arrays. The ‘operation’ is often as simple as a straight addition (ILMath.add, ILMath.divide, a.s.o.). However, what is special about broadcasting is that it allows the operation even for the case where both arrays involved do not have the same number of elements.
Broadcasting in ILNumerics prior Version 4.10
In ILNumerics, broadcasting is available for long already. But prior version 4.10 it was limited to scalars operating on n-dim arrays and vectors operating on matrices. Therefore, we had used the term ‘vector expansion’ instead of broadcasting. Obviously, broadcasting can be seen as a generalization of vector expansion.
Let’s visualize the concept by considering the following matrix A:
A 1 5 9 13 17 2 6 10 14 18 3 7 11 15 19 4 8 12 16 20
Matrix A might represent 5 data points of a 4 dimensional dataset as columns. One common requirement is to apply a certain operation to all datapoints in a similar way. In order to, let’s say, scale/weight the components of each dimension by a certain factor, one would multiply each datapoint with a vector of length 4.
ILArray<double> V = new[] { 0.5, 3.0, 0.5, 1.0 };
0.5
3.0
0.5
1.0
The traditional way of implementing this operation would be to expand the scaling vector by replicating it from a single column to a matrix matching the size of A.
VExp = repmat(V, 1, 5); 0.5 0.5 0.5 0.5 0.5 3.0 3.0 3.0 3.0 3.0 0.5 0.5 0.5 0.5 0.5 1.0 1.0 1.0 1.0 1.0
Afterwards, the result can be operated with A elementwise in the common way.
ILArray<double> Result = VExp * A; 0.5 2.5 4.5 6.5 8.5 6.0 18.0 30.0 42.0 54.0 1.5 3.5 5.5 7.5 9.5 4.0 8.0 12.0 16.0 20.0
The problem with the above approach is that the vector data need to be expanded first. There is little advantage in doing so: a lot of new memory is being used up in order to store completely redundant data. We all know that memory is the biggest bottleneck today. We should prevent from lots of memory allocations whenever possible. This is where vector expansion comes into play. In ILNumerics, for long, one can prevent from the additional replication step and operate the vector on the matrix directly. Internally, the operation is implemented in a very efficient way, without replicating any data, without allocating new memory.
ILArray<double> Result = V * A; 0.5 2.5 4.5 6.5 8.5 6.0 18.0 30.0 42.0 54.0 1.5 3.5 5.5 7.5 9.5 4.0 8.0 12.0 16.0 20.0
Generalizing for n-Dimensions
Representing data as matrices is very popular in scientific computing. However, if the data are stored into arrays of other shapes, having more than two dimensions, one had to fall back to repmatting in order for the binary operation to succeed. This nuissance has been removed in version 4.10.
Now it is possible to apply broadcasting to two arrays of any matching shape – without the need for using repmat. In order for two arrays to ‘match‘ in the binary operation, the following rules must be fullfilled:
- All corresponding dimensions of both arrays must match.
- In order for two corresponding dimensions to match,
- both dimensions must be of the same length, or
- one of the dimensions must be of length 1.
An example of two matching arrays would be a vector running along the 3rd dimension and a 3 dimensional array:
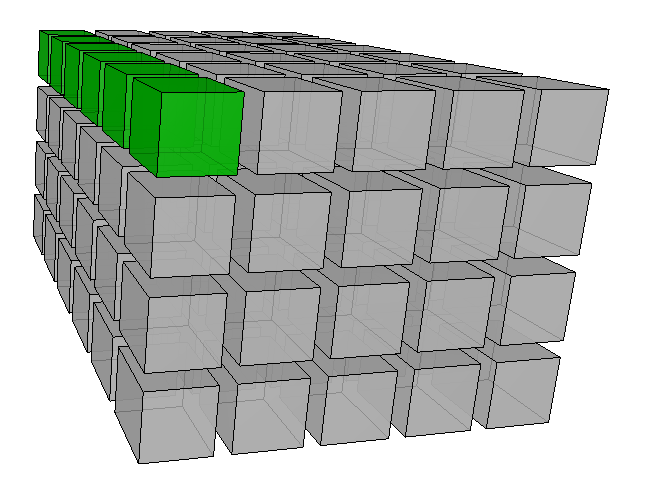 In the above image the vector (green) has the same length as the corresponding dimension of the 3D array (gray). The size of the vector is [1 x 1 x 6]. The size of the 3D array is [4 x 5 x 6]. Hence, any dimension of both, the vector and the 3D array ‘match’ in terms of broadcasting. A broadcasting operation for both, the vector and the array would give the same result as if the vector would be replicated along the 1st and the 2nd dimensions. The first element will serve all elements in the first 4 x 5 slice in the 1-2 plane. This slice is marked red in the next image:
In the above image the vector (green) has the same length as the corresponding dimension of the 3D array (gray). The size of the vector is [1 x 1 x 6]. The size of the 3D array is [4 x 5 x 6]. Hence, any dimension of both, the vector and the 3D array ‘match’ in terms of broadcasting. A broadcasting operation for both, the vector and the array would give the same result as if the vector would be replicated along the 1st and the 2nd dimensions. The first element will serve all elements in the first 4 x 5 slice in the 1-2 plane. This slice is marked red in the next image:  Note that all red elements here derive from the same value – from the first element of the green vector. The same is true for all other vector elements: they fill corresponding slices on the 3D array along the 3rd dimension.
Note that all red elements here derive from the same value – from the first element of the green vector. The same is true for all other vector elements: they fill corresponding slices on the 3D array along the 3rd dimension.
Slowly, a huge performance advantage of broadcasting becomes clear: the amount of memory saved explodes when more, longer dimensions are involved.
Special Case: Broadcasting on Vectors
In the most general case and if broadcasting is blindly applied, the following special case potentially causes issues. Consider two vectors, one row vector and one column vector being provided as input parameters to a binary operation. In ILNumerics, every array carries at least two dimensions. A column vector of length 4 is considered an array of size [4 x 1]. A row vector of length 5 is considered an array of size [1 x 5]. In fact, any two vectors match according to the general broadcasting rules.
As a consequence operating a row vector [1 x 5] with a column vector [4 x 1] results in a matrix [4 x 5]. The row vector is getting ‘replicated’ (again, without really executing the replication) four times along the 1st dimension, and the column vector 5 times along the rows.
array(new[] {1.0,2.0,3.0,4.0,5.0}, 1, 5) +array(new[] {1.0,2.0,3.0,4.0}, 4, 1)
<Double> [4,5]
[0]: 2 3 4 5 6
[1]: 3 4 5 6 7
[2]: 4 5 6 7 8
[3]: 5 6 7 8 9
Note, in order for the above code example to work, one needs to apply a certain switch:
Settings.BroadcastCompatibilityMode = false;
The reason is that in the traditional version of ILNumerics (just like in Matlab and Octave) the above code would simply not execute but throw an exception instead. Originally, binary operations on vectors would ignore the fact that vectors are matrices and only take the length of the vectors into account, operating on the corresponding elements if the length of both vectors do match. Now, in order to keep compatibility for existing applications, we kept the former behavior.
The new switch ‘Settings.BroadcastCompatibilityMode’ by default is set to ‘true’. This will cause the Computing Engine to throw an exception when two vectors of inequal length are provided to binary operators. Applying vectors of the same length (regardless of their orientation) will result in a vector of the same length.
If the ‘Settings.BroadcastCompatibilityMode’ switch is set to ‘false’ then general broadcasting is applied in all cases according to the above rules – even on vectors. For the earlier vector example this leads to the resulting matrix as shown above: operating a row on a column vector expands both vectors and gives a matrix of corresponding size.
Further reading: binary operators, online documentation
