ILNumerics Accelerator: Getting Started, Part III

Array Pipelining for Faster Fast Fourier Transforms (FFFT)

Continueing our series of getting started guides for the ILNumerics Accelerator compiler. In former parts we used the Accelerator to speed up some simple array expressions. We have also used the new array compiler to gain performance in the k-means algorithm. Now, we are going to deal with another important target for optimizations: high level functions.

The term 'high' refers to complexity: such functions are more complex than the elementary functions we have accelerated before. High level functions perform more complex tasks but still often serve as building blocks in own algorithms. Examples of such functions are: matrix multiply, fft, matrix decompositions and other linear algebra. 

Here, we pick the FFT function for computing the fast fourier transform of a matrix A and compare the speed of Intel's MKL FFT implementation alone with ILNumerics Accelerator. Below, we will demonstrate this example step by step. You may also download the whole example project here.

ILNumerics FFT API

ILNumerics offers the Fast Fourier Transform in two flavors: a managed implementation and a native implementation. The managed version was translated from the official FORTRAN codes into CIL codes (using ILNumerics in-house F2NET compiler). These codes work without any dependency on unmanaged code or native libraries. They bring industrial grade robustness together with compatibility with all platforms supporting .NET. ILNumerics.ILMath.fft() functions use the managed implementation if no native version is found at application start.

The native implementation calls into the quasi standard for linear algebra / FFT routines today: Intels Math Kernel Library (MKL) is a popular FFT implementation, optimized for recent hardware features. It is used under the hood by many scientific tools, regardless if they are based on python, Matlab, C or FORTRAN codes. ILNumerics facilitates the use of MKL for 64bit applications on Windows and Linux by simply adding the ILNumerics.Core.Native nuget package to your project. 

The ILNumerics user conveniently accesses both versions by the common interface: ILMath.fft() and ILMath.ifft().

Performance Baseline: FFT using Intel's MKL

We start with a fresh, empty C# Console application with the nuget package dependencies: ILNumerics.Computing and ILNumerics.Core.Native. Our test computer runs Visual Studio 2022, .NET 8.0, Windows 11, x64, Intel i7-12700K, 3.60 GHz. 

Replace the auto-created Program.cs content with the following code: 

In line 1 we disable the ILNumerics Accelerator: we want to measure the native speed of the MKL at first. After the using import directives follows some boilerplate code: creation of test data in line 8 and 9. Our data matrix A holds 1000 x 1000 double precision floating point elements.

For measuring we calculate the array expression abs(ifft(fft(A))). I.e.: perform the 1-dimensional fft on the matrix A, immediately perform the inverse transform, calculate the magnitude and assign the result to the variable R. R is now equal to the source matrix A, subject of floating point rounding errors. 

To get a more robust measurment result we execute this expression 10 times and calculate the average time required for each computation of R. The whole measurement is repeated 10 times, individual times are displayed below. Make sure to run this test in Release mode, without a debugger attached:  

ILNumerics base implementation calculates this expression in roughly 16 ms, using the MKL's FFT implementation. 

Accelerating (already) Fast Fourier Transforms

How can we make it faster? Let the ILNumerics Accelerator figure it out! Make sure to add the ILNumerics Accelerator.Command nuget package to your project. Using the Nuget Package Manager, include prereleases into your search while the Accelerator is still in preview. Then, add the following code to the Program.cs file started above: 

This code is added to the measurement test above, so that we can easily compare both test results.

The new measurement strategy is very much the same: average 10 executions of the array expression, repeat the measurement 10 times to display one row of measurement values. This time we create 5 such rows to see, how stable the performance stays over time. Further, and to make the measurement more fair we wait for all compuations to Finish() after each inner loop (10 executions). 

Running this in Release mode and without a debugger attached, gave the following result: 

The accelerated code was ~2.5 times faster than the non-accelerated, pure MKL version. Also, note that the measured times undergo very small variations only - a hint to what potentially causes the superior performance.

Discussion 

The cause of the better speed of the ILNumerics Accelerator is - again: more efficient parallelization. The factor of ~2.5 times better speed might lead us to the assumption that the MKL version did not compute the FFT on multiple cores but ILNumerics Accelerator would. However, the situation is actually more interesting.

Let's revisit Intel's VTune performance profiler! Interesting regions while executing our test app are shown below:

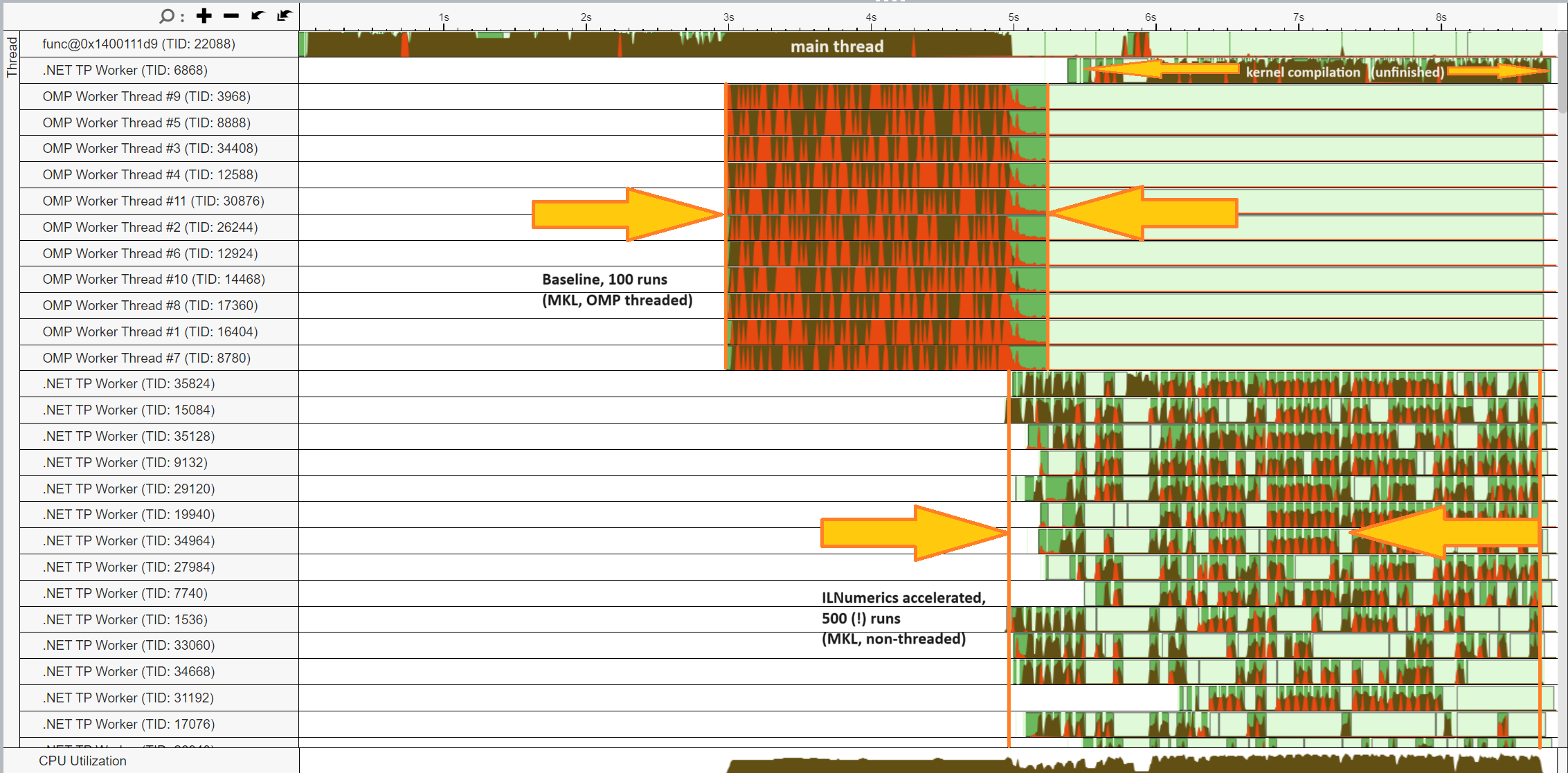
A lot of work is done on the main thread (at the very top of the image). Brown regions mark CPU activity (usually a good thing). Synchronization activity is marked red (often a performance bottleneck). 

While computing the baseline version part of our measurement app the MKL spans 11 OpenMP worker threads. They ought to compute the 100 forward-backward FFTs on as many threads as possible. Unfortunately, a lot of contention (red regions) is happening. Further, the main thread remains very busy waiting for many intermediate results. Note, that MKL attempts to parallelize each invocation of fft(A), where A is a matrix [1000 x 1000]. Thus, all threads are busy computing one single invocation result.

The accelerated part following the baseline version shows a different picture: it computes 5 times as many FFTs in ~1.5 more time when compared to baseline. The main thread basically remains idle for the whole time. The main optimization here is array pipelining:

Array pipelining calculates many invocations of fft(A) in parallel, while each invocation is calculated on a single thread. No parallelization is used within the MKL. The Accelerator identifies and uses parallel potential by deferring the actual result calculation at runtime. Instead of spending time in doing fft calculations, it just prepares the array instructions for later, asynchronous processing. This allows the main thread to quickly visit subsequent instructions and to prepare them as well. The instruction results are computed asynchronously and as soon as their input data become ready.

Thus, individual workloads become larger and can be more efficiently be calculated. Threads are no longer synchronized after each instruction. Multiple, subsequent instructions (fft, ifft, abs) are merged into a single segment. They reflect a single branch in the acyclic graph of dependencies and are asynchronously executed as soon as its input data become ready.

Overall, the accelerated version shows much less contention / synchronization and fewer wait times. It is fair to say that it manages to parallelize the array expressions more efficiently. 

There is yet another interesting bit: while we were measuring the performance of our accelerated FFTs the Accelerator was still busy compiling low-level kernel codes for some instructions from our measurement app. This compilation is seen on the second thread from the top. It was still compiling when the app finished, hence, consumed precise CPU slots without helping much. 

Validation

Let's be serious and validate our assumptions! We modified the source code to measure 100 runs of the FFT expressions at once. This should limit the impact of the unnecessary (except for measurment purposes) Finish() synchronization instructions. Further, we have concentrated on the array expression as measurement target and exluded all surrounding code from acceleration. This should prevent the kernel compiler from kicking in. Note, that in a production system you would try not to 'filter out' any regions manually! It is commonly better to leave such decisions to the Accelerator.

The new, slightly modified code: 

It gives a result similar to this: 

This gives us a further, small improvement: we have almost reached a 3 times speed-up now. Or, to put it in other words: The parallelization applied by ILNumerics Accelerator is three times more efficient than the internal, hand-tuned parallelization inside MKL on our test machine.

Discussion II

The internal parallelization as used by the MKL is very common today. But it does not perform too well - as we have seen. Since all parallel potential must be collected from a single array instruction invocation, since the data must be split and distributed onto multiple threads, processed asynchronously, since the main thread has to wait for the results ... all this is only efficient when the workload is large. Really large.

A workload becomes large for very large data or for costly array instructions. FFT, having O(N log N) complexity, is not a bad candidate here. Also, it is an example of an 'embarrasingly parallel' workload, since ffts for each column from the input matrix are computed independently. However, imagine to use this scheme for more simple, O(N) array instructions, like array subtraction A - B: it only pays off for huge array sizes, with millions or billions of elements.

How does ILNumerics array pipelining behaves for various data sizes?

Taking our example further, we have measured various array sizes. The same forward - backward FFT expression is calculated and the fastest execution time is used for plotting the results in context: 

This chart uses logarithmic axes scaling. It displays the minimum execution times measured for the threaded MKL (blue line) together with the minimum execution times for the ILNumerics Accelerator version (orange line). The thick red line shows the speed-up factor for the accelerated FFT. Over the whole range of workload sizes, from [100 x 100] ... [5.000 x 5.000] double precision elements the accelerated code shows a very stable speed-up factor of ~3 times, compared to the traditional MKL parallelization. Note, that some workloads bring even much better execution speed, especially such workloads associated with relatively moderate data sizes (here: 200 x 200 elements). 

Conclusion

ILNumerics Accelerator executes subsequent array instructions via array pipelining. The main thread only manages the setup of the pipelines. The workload is handled by individual threads concurrently. The workload in array pipelines is usually much larger than for traditional, single array instruction parallelization. Not, because we use larger data, but because more array instructions are handled within a single execution path ( = pipe). Thus, data sizes are not split into smaller, independent chunks and the scheme applies efficiently for large and small data. Lastly, scheduling is also more efficient, in that starting new chunks is automatically triggered by the completion of input data dependencies. 

All this enables ILNumerics Accelerator to compute the array expressions significantly faster. We need to emphasize, that both: accelerated code and non-accelerated code use the FFT from the MKL libraries. This example demonstrates, that ILNumerics Accelerator enables to accelerate existing code and even native libraries by more efficiently distributing workloads onto parallel compute resources on a higher level of abstraction (multiple array instructions scope) compared to traditional parallelization approaches, which use single array instruction scope only.