Constrained Optimization in .NET (C# and Visual Basic)

In constrained optimization a minimium of a nonlinear scalar function is found which satisfies certain conditions ('constraints'), namely bound constraints (sometimes referred to as box constraints), equalty and inequalty constraints. ILNumerics Optimization Toolbox solves these kind of problems by modifying the objective function in a way that the resulting problem can be solved in terms of an unconstrained optimization problem. The resulting function is than handled by means of an unconstrained optimization method.

Usage

A single common function serves as the API entry point for all constrained minimization algorithms:

ILNumerics.Optimization.fmin - common entry point for nonlinear constrained minimizations

In order to solve a constrained minimization problem, users must specify

The objective function,
An intial guess for a feasible solution and
Any number of custom defined constraints.

Just as for unconstrained optimization problems, a number of options exist which can be used to control the optimization run and to gather details of the optimization algorithm performance.

Types of Constraints

ILNumerics Optimization Toolbox recognizes bound constraints, equalty and inequalty constraints.

Bound Constraints

Optimization.fmin solves optimization problems with bounded constraints defined by

$\min_{x} f (x)$ where $f : R^{n} \to R$

subject to $lb \le x \le ub$.

Bound constraints restrict the solution to a range within lower and upper bounds. The bounds $lb$ and $ub$ are defined by use of the lowerBound and upperBound parameters to Optimization.fmin. Both are optional parameters: it is possible to define none, one, or both. Undefined bounds correspond to double.MinValue and double.MaxValue respectively.

Example

Let's consider the minimization problem

$\min_{x} f (x) = {(x - 1)}^{2},$

$2 \le x \le 3$

We target a minimum in the range [2...3] which does not include the true minimum at 1. In C# the problem is solved as follows:

A shorter form might use lamda expressions for the objective function:

This finds the minimum of $f$ inside the defined bounds:

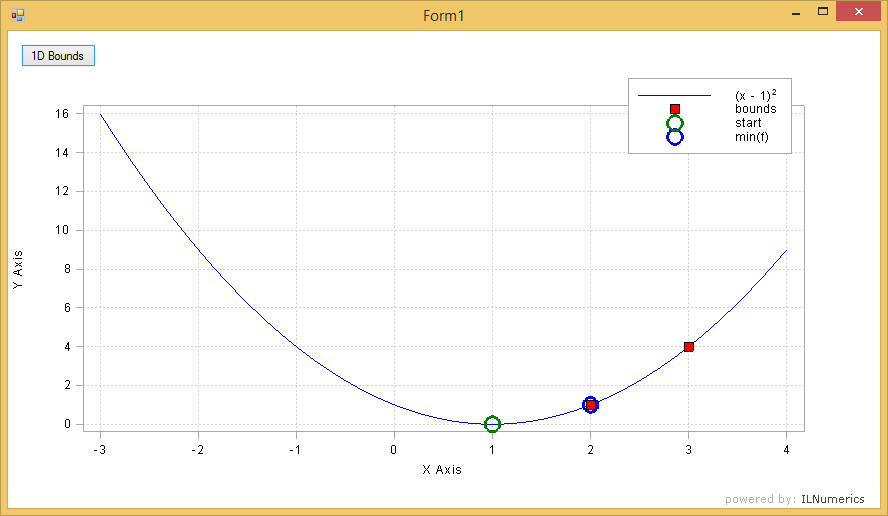
Constrained Optimization in .NET (C# and Visual Basic)

This example is part of a larger example which can be downloaded from the examples section.

Equality Constraints

Equalty constraints are defined as

$\min_{x} f (x)$ where $f : R^{n} \to R^{q}$

subject to $eq(x) = 0,\, eq : \mathbb{R}^n → \mathbb{R}^q$

Only solutions are allowed, which satisfy the equalty constraint equation. The constraint equation must be implemented in a form which rewrites the constraint to the form $eq(x) = \vec0$. That is: the equalty constraint $y = 2 x + 5$ is rewritten as $y - 2x - 5 = 0$.

Example

The following example computes the minimizer for the function $$(x - 1)^2 + (y + 2)^2 - 4$$ As solution only those values are accepted, which lay on the line $$y = 2 x$$ We state the objective function and reformulate the equalty constraint as $2x - y = 0$:

The complete example from the examples section plots the objective function, the equalty constraint, intermediate positions on the path to the result and the computed minimizer:

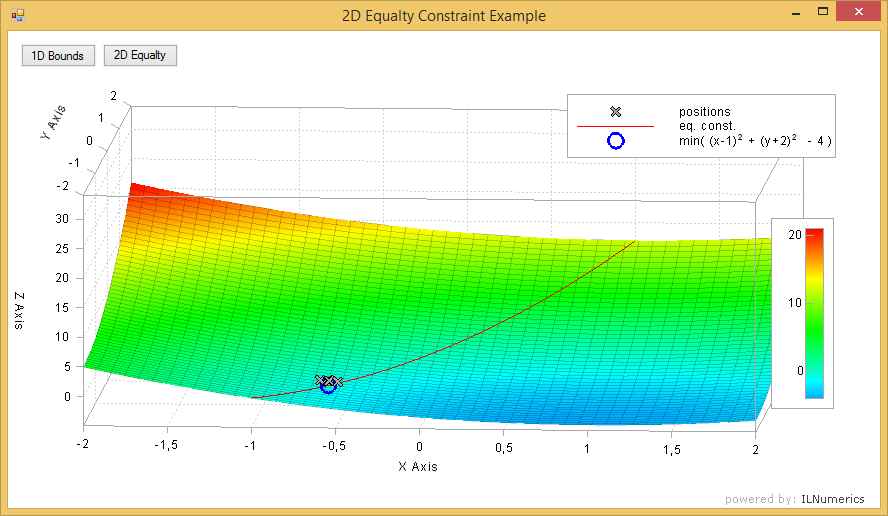
2D constrained optimization in .NET (C# and Visual Basic)

Note how the objective function myFunc2DEqual was defined in vectorial form here. This gives more options for plotting purposes and further handling, since it allows the evaluation of multiple datapoints at the same time. Hoewever, for the minimizer computation, vectorization is not necessary! All minimization algorithms are guaranteed to call the objective function with a single (intermediate) position vector only. Thus, the function could have been defined in scalar form:

The number of equalty constraints is not limited. Functions implementing equalty constraints expect input arrays (column vectors) of length $n$ and return column vectors of length $q$. Each component of the column vector returned corresponds to one single equalty constraint.

Inequality Constraints

The third type of constrained minimization problems is defined as:

$\min_{x} f (x)$ where $f : R^{n} \to R^{m}$

subject to $ineq(x) \lt \vec0,\, ineq : \mathbb{R}^n → \mathbb{R}^m$

This limits the feasible set of solutions to a certain definition range. Again, in order to be usefull, the inequalty constraint must be implemented in the form $ineq(x) = \vec0$ and reformulated, if necessary.

Example

We state the optimization problem

$f(x_0, x_1) = x_0^2 + x_0x_1 - x_1^2$

$subject\,to\, (x_0-1)^2 + (x_1-1)^2 \lt 1$

Here, the solution is constrained to the circle area around the point [1,1] with the radius 1. In order to implement the inequalty constraint function we reformulate:

$(x_0-1)^2 + (x_1-1)^2 - 1 \lt 0$

and implement the problem:

After 3 iterations the solution is found at the edge of the circle area described by the inequalty constraint:

inequality constrained optimization in .NET (C# and Visual Basic)

The complete example can be downloaded from the examples section.

Combining Constraints

All types of constraints can be combined arbitrarily. We could add bound constraints to the inequalty constraint example above and limit the solution to the subpart of the circle where $x_1 \le 1.5$.

This gives:

Controlling the Algorithm

The following options exist for influencing the progress of the algorithm:

The optional maxIter parameter is used to limit the overall iteration count. Common values range from 25 to 1000. If the algorithm hits the maxIter limit, this is usually a good indication of a difficult problem, too tight constraints or a non-existent or non-feasible solution or a too low error tolerance value requested. The default value for maxIter for constrained optimization is 500. Note that 'iteration' refers to the iteration steps carried out on the optimal modified objective function (Lagrangian). It does not take into account the steps needed to minimize the Lagrangian formulation for each individual step.
tolX is an optional parameter specifying one necessary exit criterion from the iteration loop. For constraint minimization problems a solution is considered optimal, when the current solution cannot be improved by further iterations. To put it mathematically: the 2-norm of the difference between subsequent intermediate solutions is less or equal to tolX: $ ||x_{cur} - x_{last}||^2 <= tolX$. Internally, tol is scaled for robustness. tolX is also used to control the corresponding tolX parameter for the subproblem minimization as described in Unconstrained Optimization. The default value for tolX is $1e^{-8}$.
tol controls the precision of the solutions of the subproblems to be minimized in each iteration step. See: tol in Unconstrained Optimization. The default value for tol is $1e^{-8}$.

Gathering Progress Information

Optimization.fmin provides three parameters which are used to get extended information about the algorithm run. The iterations and the gradientNorm parameters provide the intermediate solutions and the norm of the Lagrangian gradient from each major iteration step - after the function returns. Their application is identical to the corresponding parameters in Unconstrained Optimization.

Iteration Callback

The iterations parameter gives the intermediate solution vectors found in each iteration step. In order to gain even more information about how these intermediate solutions have been found, users can register a callback function which gets called by fmin in each iteration step.

The callback parameter expects a user defined function with the following signature:

The FminCallbackInfo class provides a number of readonly properties which describe the current iteration step:

IterCount - upwards counting number of the major iteration. Each time the callback gets called, iterCount is incremented.
XSub is the current intermediate solution of the subproblem solved. This is not a solution of the constrained optimization problem defined. Instead XSub describes a solution of the unconstrained subproblem stated by the Lagrangian in each iteration step.
GradL is the gradient of the Lagrangian at position XSub. Each major iteration in a constrained optimization problem involves the minimization of an unconstrained subproblem (via the Lagrangian). The minimum of that subproblem is expected to have a gradient of 0. The actual value returned in GradL serves as a hint for the quality of the solution of the current subproblem.
DistX is the difference between the current value of XSub and the value from the last iteration. Decreasing values for DistX in most situations indicate progress towards an optimal solution. DistX gives the 2-norm of the difference.
EqConst - if equalty constraints were provided for fmin, this parameter gives the evaluation of these constraints at XSub. The absolute value of EqConst serves as a measure for the violation of the equalty constraint at the current intermediate solution XSub.
IneqConst - if inequalty constraints were provided for fmin, this parameter gives the evaluation of these constraints at XSub. If the value of IneqConst is larger than 0 this serves as a measure for the violation of the constraints at the current intermediate solution.
FCost - the cost function gives a measure of the penalty introduced by the constraints (bound-, equalty-, and inequalty constraints) to the current solution value. Since fmin() tries to minimize these violations decreasing values of FCost potentially indicate a progress towards an optimal solution. However, it is normal for an algorithm run to create non constantly decreasing values.
Cancel - The implementor of the custom function receiving the FminCallbackInfo object can cancel the current minimization algorithm run by setting the Cancel flag to true. This will lead to the immediate cancellation of the iterations and Optimization.fmin returns normally, as if regular exit criteria would have been met.

Limitations

Optimization.fmin currently is not able to solve the following special problems:

Linear objective function without effective bound- / equalty- / or inequalty constraints. Consider using linsolve instead.
Objective functions having at least one saddle point in the feasible area defined by the constraints may cause problems. It is recommended to reformulate the problem (the constraints) in order to exlude the saddle point from the defintion space. Alternatively, one may relocate the initial guess closer to the anticipated solution and exluce the saddle point from the search path.

Technical Details

ILNumerics.Optimization.fmin() reformulates the provided constrained problem into an unconstrained one. The Powell-Hestenes-Rockafellar augmented lagrangian multiplier method turns the objective function into a modified version which penalizes violations of the constraints. Each iteration step for fmin() solves an unconstrained optimization problem for finding the minimum of the Lagrangian function. With feasible constraints defined, the objective function is not required to be non-linear.

All unconstrained optimization solvers can be used to find the minimimum of the Lagrangian in each iteration. BFGS is the most popular one here. Bound constraints are not taken into account by considering them as inequalty constraints. Rather the intermediate solutions are projected onto the given bounds in each iteration step.

References

Stephen Wright, Jorge Nocedal, "Numerical Optimization", Springer Series in Operations Research and Financial Engineering, 2006

Biggs, M.C., "Constrained Minimization Using Recursive Quadratic Programming", Towards Global Optimization (L.C.W. Dixon and G.P. Szergo), North-Holland, 1975

Coleman, T.F., Y. Li, "A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on some of the Variables", SIAM Journal on Optimization, Vol. 6, Number 4, p. 1040 to 1053, 1996

Powell, M.J.D., "A fast Algorithm for nonlinearly constrained Optimization Calculation", Numerical Analysis, G.A.Watson ed., Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978

ILNumerics Optimization Toolbox is available for individual purchase. API reference documentation is available here.