Fast Interpolation in .NET (C#, Visual Basic)
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points. There are many different interpolation methods for various situations. The ILNumerics Interpolation Toolbox provides highly efficient algorithms in a very convenient way.
The algorithms provided are best categorized by the origin of the sampled data. Functions are provided for data which were sampled from a grid and for unstructured data sets (scattered data).
ILNumerics Interpolation Toolbox allows the interpolation of data of any dimensionality. However, one-dimensional interpolation methods receive their own section.
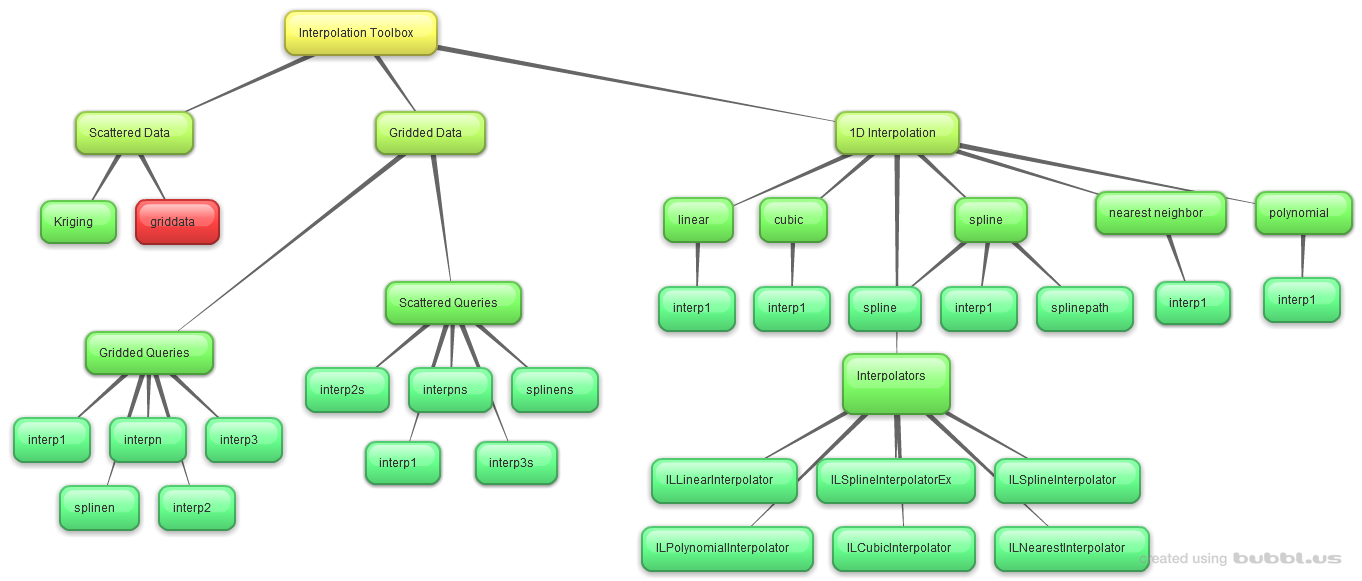
The image below serves as a rough decision tree for selecting an appropriate interpolation function.
Read the whole section for a more in-depth documentation.
Interpolation Overview
Interpolation is a mathematical method of estimating values of an unknown function based on measured or otherwise known values at known positions. Basically, a function of a certain type is constructed from the given data and evaluated at the new positions in order to get an estimate of the values at these positions - without having to perform a new measurement. Obviously, the newly computed values will be more exact in the close proximity of the known points. However, the overall error of the estimation result strongly depends on the interpolation method used and serves as an important criteria for the selection and validation of individual interpolation methods.
Other criteria are: the smoothness of the resulting function, the computational effort needed for computing the results, and – especially for interpolation in higher dimensions – the memory requirements. See the section about one-dimensional interpolation functions for a comparison of all fundamental interpolation methods provided with ILNumerics Interpolation Toolbox.
Next to the common interpolation functions (linear, spline etc.) on 1D and gridded data, a more general, flexible, yet efficient approach is provided by kriging interpolation - a method which is able to compete with the popular spline interpolation regarding smoothness, efficiency and its unique ability to provide error information.
Quick Start - Function Overview
The following table gives you a jump start to the functions in the ILNumerics.Toolboxes.Interpolation class.
| Function | Description | Details |
|---|---|---|
| Gridded data | ||
| interp1 | Single entry point for all 1D methods. | Manual / apidoc |
| interp2 | Two-dimensional interpolation, all methods. | Manual / apidoc |
| interp3 | Three-dimensional interpolation, all methods. | Manual / apidoc |
| interpn | N-dimensional interpolation, all methods. | Manual / apidoc |
| Scattered queries on gridded data | ||
| interp2s | Scattered queries on a two-dimensional grid. | Manual / apidoc |
| interp3s | Scattered queries on a three-dimensional grid. | Manual / apidoc |
| interpns | Scattered queries on an n-dimensional grid. | Manual / apidoc |
| Spline functions | ||
| spline | One-dimensional spline interpolation. | Manual / apidoc |
| splinen | N-dimensional spline interpolation. | Manual / apidoc |
| splinens | Scattered queries on n-dimensional grids, using spline interpolation. | Manual / apidoc |
| splinepath | Connect scattered points in n dimensions with a spline line. | Manual / apidoc |
| General scattered and gridded data, any dimensionality | ||
| kriging | Interpolation from scattered data. Also applicable for general 1D ... N-D interpolation, also for gridded data. | Manual / apidoc |
One-dimensional Interpolation
Interpolation of new data points from a one-dimensional set of existing (known) data points forms kind of a foundation for many very common situations. ILNumerics Interpolation Toolbox provides an extensive set of related functionality. This includes all popular interpolation techniques, like: linear, cubic, spline interpolation and more. Next to the common function interface Interpolation.interp1() interpolator objects are provided for the fast and efficient computation of multiple data sets in parallel. For spline interpolation, a specialized interface is provided. The following documentation sections are available for one-dimensional interpolation functions:
- Overview of one-dimensional interpolation functions.
- Function interface for one-dimensional interpolation, interp1(apidoc)
- 1D interpolator objects for efficient interpolation of large data.
- 1D spline interpolation, spline(), (apidoc)
- 1D kriging interpolation, kriging()
Gridded Data Interpolation in .NET
If the known data were sampled/ measured on a rectilinear grid one can interpolate new points from them very efficiently. The set of new query points may itself form a rectilinear grid. Or these points can be distributed arbitrarily over the sampled domain:
Computing gridded data from a sampled grid
Computing a rectilinear grid of new samples (green) from a grid of existing samples (red).
Computing scattered data from a sampled grid
Computing scattered points (green) from a rectilinear grid of sampled data (red).
The following sections deal with gridded data interpolation. Corresponding class reference links are provided:
- Introduction to Gridded Data Interpolation
- Grids from gridded Data - describes how to interpolate new query points which are itself aligned on a rectilinear grid. [class references: interp2, interp3, interpn, splinen]
- Scattered Points from gridded Data - shows how to compute scattered data from a set of values, measured from a grid. [class references: interp2s, interp3s, interpns, splinens]
Scattered Data Interpolation in .NET
Data which are measured at arbitrary, non-structured positions are common in many technical areas. Consider the measurement of hourly temperature at existing weather stations. Another example are properties of the ground measured from drilling on a large area at positions which are usually not feasible to be placed at regular grid positions. Data retrieved from those measurements are called scattered data. The following function can be used to derive neighboring values or to create a grid of interpolated values for visualization purposes:
There exist an example for kriging interpolation which demonstrates one way to handle too large data for kriging by tiling. The example is found in the examples section.