ILNumerics^® Optimization Toolbox - Quick Start Guide

This quick start guide will help you to get up and running with common optimization problems. Consult the subsequent chapters of the online documentation for more in-depth information.

Optimization of a Function with two Variables

Consider the following function as an example of a common optimization problem:$$f = e^{0.001 (y^2 + (x - 2)^2)}$$

ILNumerics.Optimization.fmin() finds the minimum of this function at [2,0]. This is the global minimum, since the function has only one minimum:

We allow a solution in the whole definition space (R²). No restriction (constraint) exists. Therefore, this problem is an unconstrained optimization problem. Read more about handling unconstrained problems here: Unconstrained Optimization.

The objective function has a single return value. In general, finding the minimum of such problems involves two main steps:

1. Implement the objective function.
2. Specify a starting point to begin searching for the minimum.

Constrained Optimization

Let's suppose that for some reasons the optimal solution for the above problem would be restricted to the subspace of R² having an x coordinate larger than 3.0 and an y coordinate larger than -1. We can find the minimum of such constrained optimization problem with the same fmin() function:

Similarly, upper bounds for each dimension can be specified using the upperBound parameter. The constrained solver is capable of handling bound constraints, equalty and inequalty constraints.

Read more here: Constrained Optimization

Nonlinear Least Squares Optimization

Maybe the most popular application for nonlinear least square problems is data fitting. The following complete example fits a polynomial model to data values created from a sinosoidal function (with some noise). The example is also found in the example projects section.

Output created:

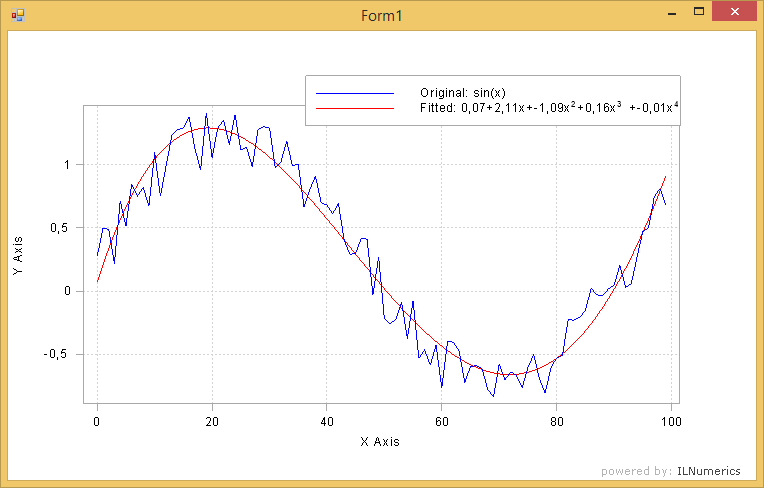
Read more about Nonlinear Least Squares methods in ILNumerics.

ILNumerics Optimization Toolbox is available for individual purchase.