tgt

3D Surface Plots in .NET (C# and Visual Basic)

3D Surface Plots in .NET (C# and Visual Basic) are used to visualize arbitrary rectangular grids of points in 3D space. Each element in the grid gets a point in 3D space assigned. In the simplest case, only the Z coordinates of the points are defined. X and Y coordinates are added automatically in order to create an equally spaced grid of connected points – forming a surface of the ‘heights’ of Z.

More complex surfaces allow the definition of individual colors for every grid point as well as individual X and Y coordinates. This allows for the creation of 4 dimensional (3d space + 1 color) arbitrary shaped surfaces. At the end of this section, examples for parametric surfaces are presented.

Surfaces are represented by the class ILNumerics.Drawing.Plotting.Surface. They are made out of:

A fill area Surface.Fill, filling the area within 4 neighboring grid points,
A wireframe Surface.Wireframe connecting direct neighbors with lines.

Fill and Wireframe are regular shapes (Triangles and Lines), hence are completely configurable: colors, visibility and line styles.

3D Surface Plots: Examples

The most simple method to setup a 3D surface is to provide Z values for the grid points only. Such values can be specified by a matrix of concrete values or as a height function. ILNumerics creates a regular grid and computes default values for the X and Y directions.

One example using an analytical function for the height values:

The ranges for the X and the Y axis are configurable, though. The next example creates a surface based on the same function and specifies a grid ranging from -2 to 10 for the X axis and from -1 to 3 for the Y axis. The number of grid rows/ columns are also configured. Furthermore, a CFunc is given in order to compute the color for each grid point based on its X,Y tuple:

In order to get full flexibility, one can provide the Z data and the X and Y coordinates for each grid point explicitely. The following example creates a simple surface from some precomputed data (here: sinc() function) and configures colors and wireframe individually. This time, the positions for the grid points are explicitely given as a single, precomputed 3-dimensional array:

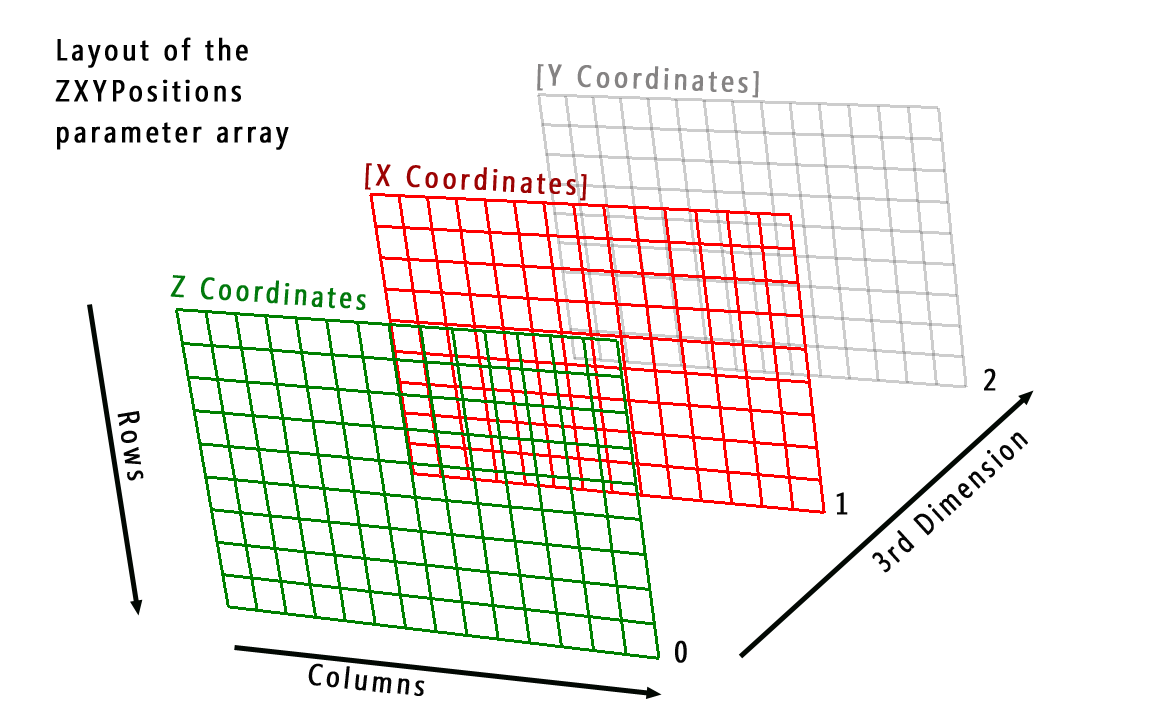
This constructor of Surface expects a ZXYPositions array with the coordinates for the grid points: coordinates of the grid points are to be layed out as matrices. Z coordinates are obligatory. Providing X and Y coordinates is optional. Note the coordinate ordering in the ZXYPositions parameter: Z is the first ‘slice’, X and Y are in the 2nd and 3rd index of the 3rd dimension in the array:

If one of X and/or Y coordinates are omitted, an evenly spaced grid is created for the missing coordinates, starting with 0 and grid point distances of 1.

ZXY Positions Layout ILNumerics

Learn more about Surface Plots in the following Chapters:

For plotting larger data consider ILFastSurface (apidoc). See its documentation here.